Partial differential equations...
Introduction
Let \(u(x, y, t)\) be ...
The homogenous wave equation is given by
$$\frac{\partial^2 u}{\partial t^2} - c^2 (\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}) = 0$$
or
\begin{equation}
u_{tt} - c^2 (u_{xx} + u_{yy}) = 0.
\end{equation}
Physical interpretation
The wave equation is a simplified model for a vibrating string (𝑛 = 1), membrane (𝑛 = 2), or elastic solid (𝑛 = 3). In these physical interpretations 𝑢(𝑥, 𝑡) represents the displacement in some direction of the point 𝑥 at time 𝑡 ≥ 0.
1D and 2D Equations
Fixed String
...
$$
\varphi(x) := \left\{\begin{align*}
\sin^3{(\pi x)}, \quad 1 \leq x \leq3, \\
0, \quad x \in R \backslash [1, 3],
\end{align*}\right.
$$
and
$$
\psi(x) \equiv 0,
$$
for \(t \in [0, 30]\). Using the \(100\)-th partial Fourier sum, \(L = \pi \sqrt{5}\), \(a = \frac{2}{3}\)...
Animation:
Click to expand code
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
# Define constants
L = np.pi * np.sqrt(5)
a = 2 / 3
tmax = 30
x = np.linspace(0, L, 101)
t = np.linspace(0, tmax, 200)
# Define the initial condition phi(x)
def phi(x):
y = np.zeros_like(x)
y[(1 < x) & (x < 3)] = np.sin(np.pi * x[(1 < x) & (x < 3)]) ** 3
return y
# Define the initial velocity psi(x)
def psi(x):
return np.zeros_like(x)
# Define the Fourier solution for u(x, t)
def fourier_u(x, t):
y = np.zeros_like(x)
for k in range(1, 101):
Xk = np.sin(k * np.pi * x / L)
Ak = (2 / L) * np.trapezoid(phi(x) * Xk, x)
Bk = (2 / (a * k * np.pi)) * np.trapezoid(psi(x) * Xk, x)
Tk = Ak * np.cos(a * k * np.pi * t / L) + Bk * np.sin(a * k * np.pi * t / L)
y += Tk * Xk
return y
# Set up the figure for animation
fig, ax = plt.subplots(figsize=(16, 2))
ax.set_xlim(0, L)
ax.set_ylim(-1, 1)
ax.set_xlabel("x")
ax.set_ylabel("u(x, t)")
ax.set_title("String Vibration")
(line,) = ax.plot([], [], lw=2, color="r")
(marker_left,) = ax.plot([], [], "ko", markerfacecolor="k")
(marker_right,) = ax.plot([], [], "ko", markerfacecolor="k")
def init():
line.set_data([], [])
marker_left.set_data([], [])
marker_right.set_data([], [])
return line, marker_left, marker_right
def update(frame):
y = fourier_u(x, frame)
line.set_data(x, y)
marker_left.set_data([0], [y[0]])
marker_right.set_data([L], [y[-1]])
return line, marker_left, marker_right
# Create the animation
anim = FuncAnimation(fig, update, frames=len(t), init_func=init, blit=True)
anim.save("string_vibration_animation.gif", writer="pillow", fps=20)
plt.show()
Snapshots:
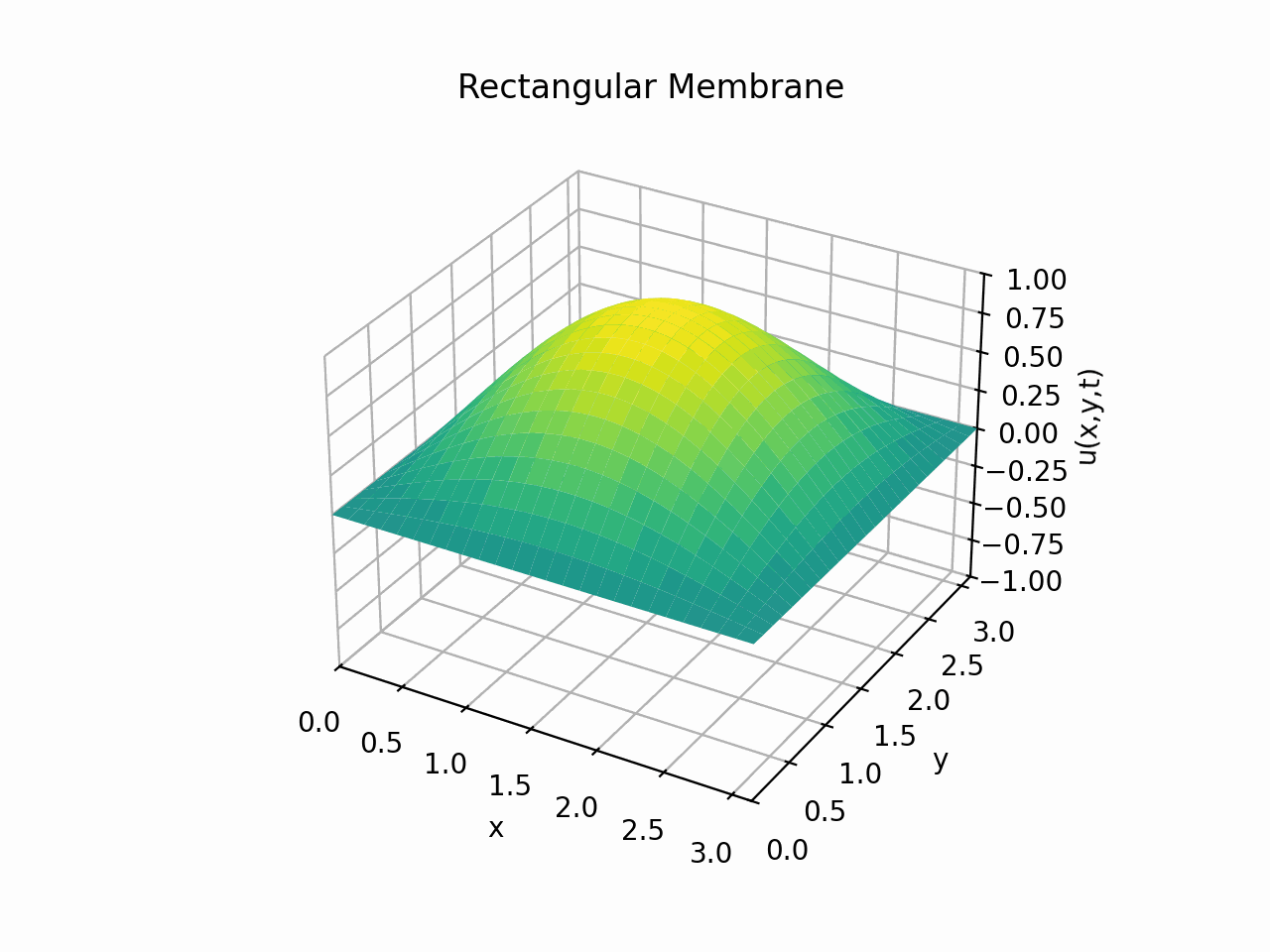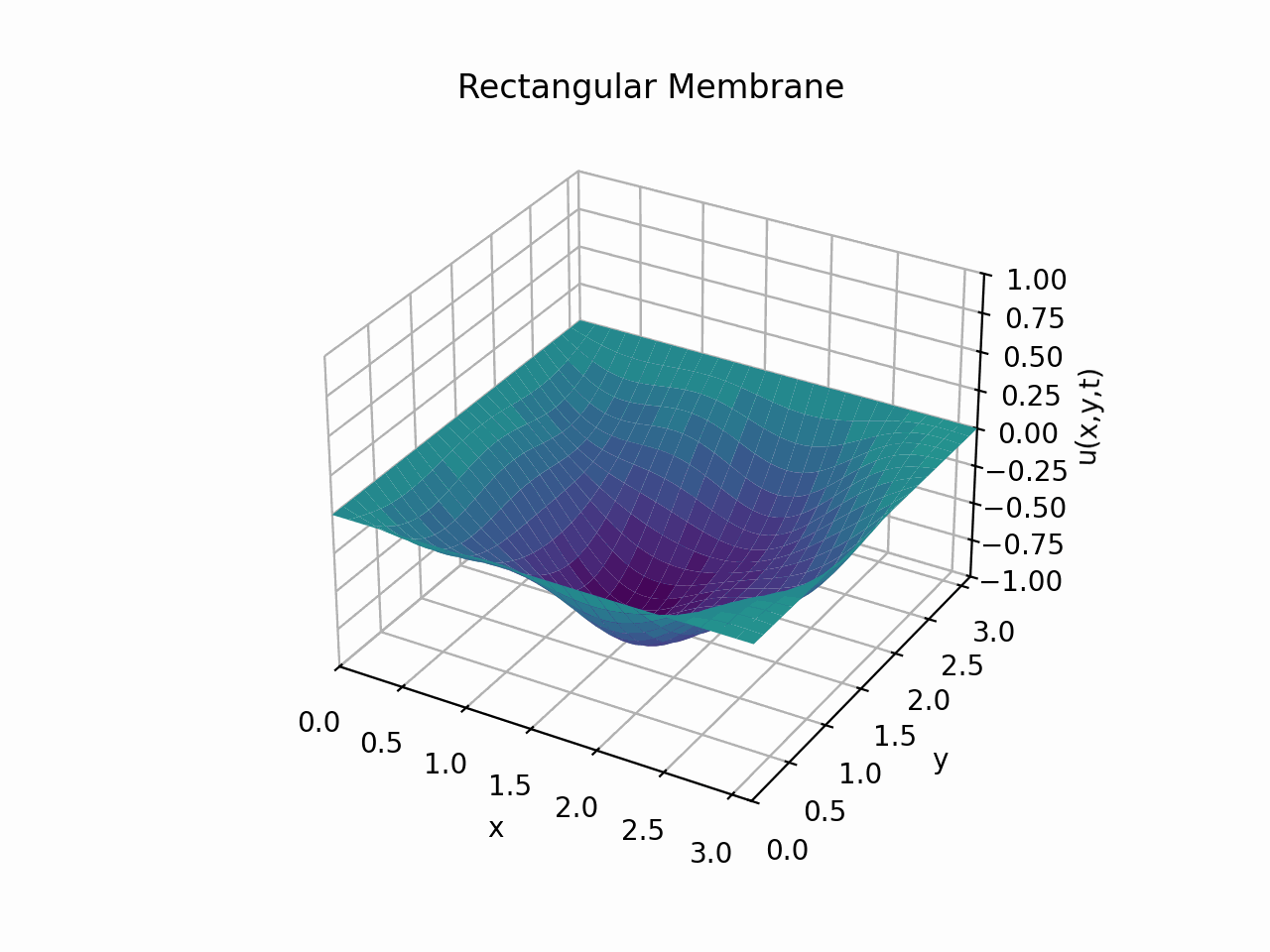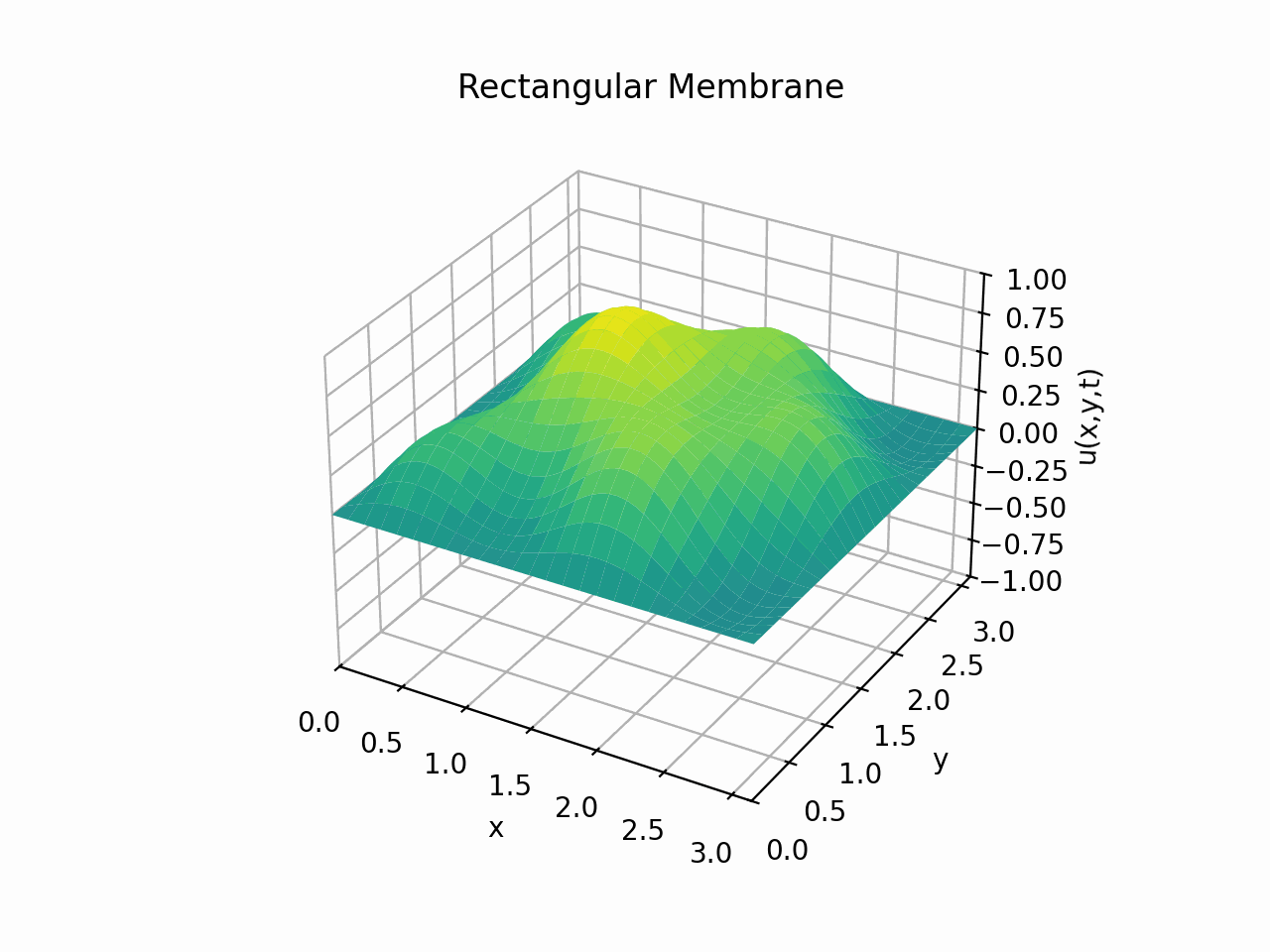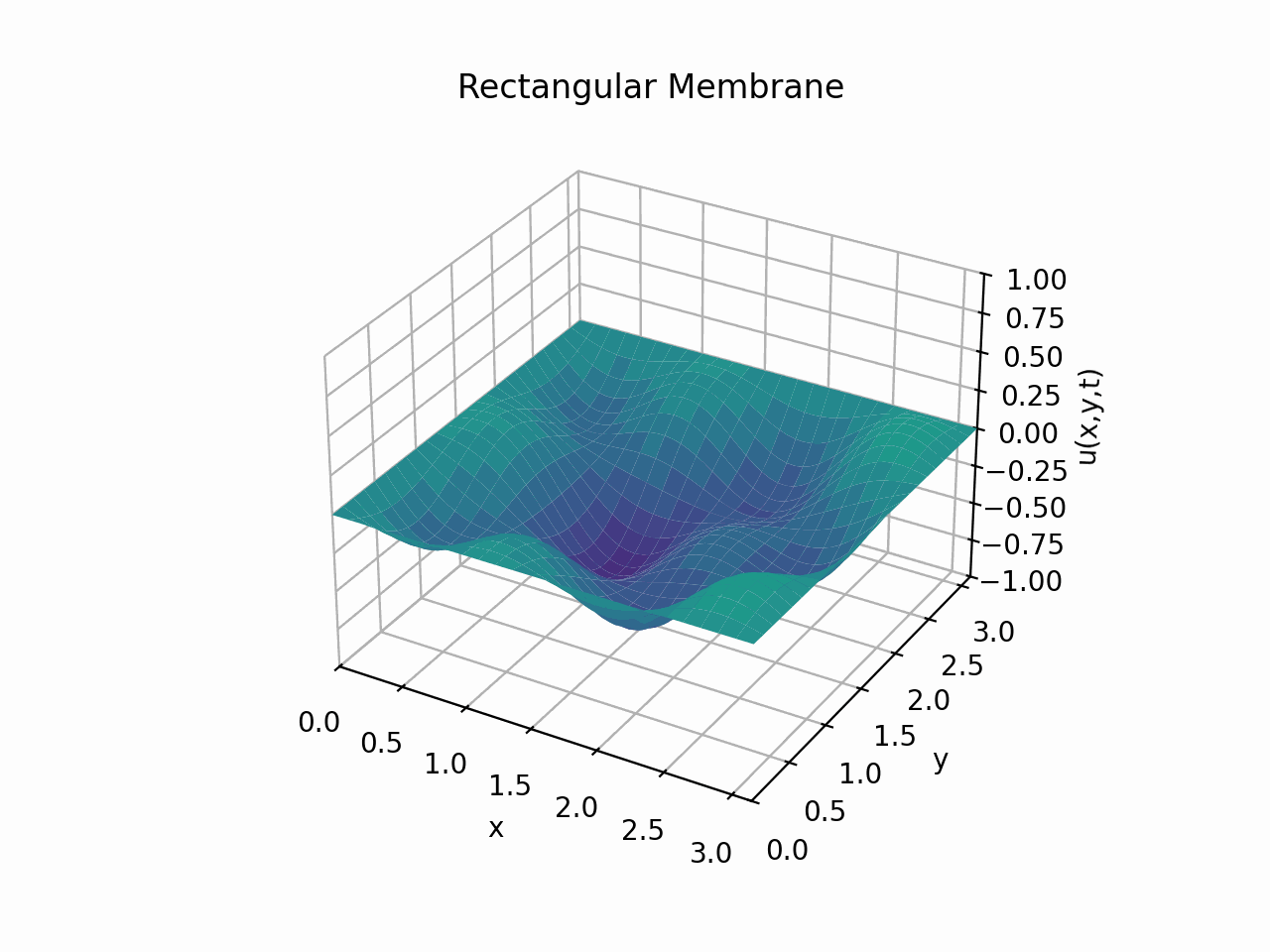
Rectangular Membrane
Pass
$$D := \{0 < x < a, 0 < y < b\}
$$
...
$$\left\{\begin{align*}
u_{tt} - c^2 (u_{xx} + u_{yy}) = 0, (x,y,t) \in G = D \times (0, +\infty), \\
u|_{t=0} = \varphi(x, y), u_t |_{t=0} = \psi(x, y), (x, y) \in \bar{D}, \\
u|_{\partial D} = 0, t \geq 0.
\end{align*}\right.$$
...
$$\varphi(x, y) \in C^3 (\bar{D}), \psi(x, y) \in C^2 (\bar{D})
$$
and ...
$$\varphi |_{\partial D} = \varphi_{xx} |_{x = 0} = \varphi_{xx} |_{x = a} = \varphi_{yy} |_{y =0} = \varphi_{yy} |_{y = b} = \psi |_{\partial D} = 0.
$$
Solution... :
$$u(x, y, t) = \sum_{n, m = 1}^{\infty} \left(A_{n, m} \cos{\sqrt{\lambda_{n, m}} ct} + B_{n, m} \sin{\sqrt{\lambda_{n, m}} ct} \right) \sin{\frac{\pi n}{a}} x \sin{\frac{\pi m}{b}} y,
$$
where
$$\lambda_{n, m} = \left(\frac{\pi n}{a} \right)^2 + \left(\frac{\pi m}{b} \right)^2.
$$
From the initial conditions it follows
$$A_{n, m} = \frac{4}{ab} \int_D \varphi(x, y) \sin{\frac{\pi n}{a}} x \sin{\frac{\pi m}{b}} y \mathrm{d}x \mathrm{d}y,
$$
and
$$B_{n, m} = \frac{4}{abc\sqrt{\lambda_{n, m}}} \int_D \psi(x, y) \sin{\frac{\pi n}{a}} x \sin{\frac{\pi m}{b}} y \mathrm{d}x \mathrm{d}y.
$$
Example 1
...
$$\left\{\begin{align*}
u_{tt} - u_{xx} - u_{yy} = 0, 0 < x < \pi, 0 < y < \pi, t > 0, \\
u|_{t=0} = \sin{x} \sin{y}, u_t |_{t=0} = \sin{4x} \sin{3y}, x, y \in (0, \pi), \\
u|_{x = 0} = 0, u|_{x = \pi} = 0, 0 < y < \pi, t > 0, \\
u|_{y = 0} = 0, u|_{y = \pi} = 0, 0 < x < \pi, t > 0.
\end{align*}\right.$$
Solution:
$$u(x, y, t) = \sum_{n, m = 1}^{\infty} \left(A_{n, m} \cos{\sqrt{\lambda_{n, m}} t} + B_{n, m} \sin{\sqrt{\lambda_{n, m}} t} \right) \sin{n} x \sin{m} y,
$$
where
$$\lambda_{n, m} = n^2 + m^2,
$$
$$A_{n, m} = \frac{4}{\pi^2} \int_0^\pi \sin{x} \sin{nx} \mathrm{d}x \int_0^\pi \sin{y} \sin{my} \mathrm{d}y,
$$
$$B_{n, m} = \frac{4}{\pi^2\sqrt{\lambda_{n, m}}} \int_0^\pi \sin{4x} \sin{nx} \mathrm{d}x \int_0^\pi \sin{3y} \sin{my} \mathrm{d}y.
$$
Therefore, \(A_{1, 1} = 1\), \(B_{4, 3} = \frac{1}{5}\), and every other coefficients is equal to \(0\). Finally,
$$u(x, y, t) = \cos{\sqrt{2}t} \sin{x} \sin{y} + \frac{1}{5} \sin{5t} \sin{4x} \sin{3y}.
$$
For \(t \in [0, 6]\):
Animation:
Click to expand code
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
def rectangular_membrane_1(t_max: int = 6):
t = np.linspace(0, t_max, 100) # Time points for animation
x = np.linspace(0, np.pi, 51) # x grid
y = np.linspace(0, np.pi, 51) # y grid
X, Y = np.meshgrid(x, y)
# Define the solution function
def solution(x, y, t):
return (
np.cos(np.sqrt(2) * t) * np.sin(x) * np.sin(y)
+ np.sin(5 * t) * np.sin(4 * x) * np.sin(3 * y) / 5
)
# Set up the figure and axis for animation
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
ax.set_xlim(0, np.pi)
ax.set_ylim(0, np.pi)
ax.set_zlim(-1, 1)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("u(x,y,t)")
ax.set_title("Rectangular Membrane")
# Update function for FuncAnimation
def update(frame):
ax.clear() # Clear the previous frame
Z = solution(X, Y, frame) # Compute the new Z values
_ = ax.plot_surface(X, Y, Z, cmap="viridis", vmin=-1, vmax=1)
ax.set_xlim(0, np.pi)
ax.set_ylim(0, np.pi)
ax.set_zlim(-1, 1)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("u(x,y,t)")
ax.set_title("Rectangular Membrane")
# Create and save the animation
anim = FuncAnimation(fig, update, frames=t, interval=50)
anim.save("rectangular_membrane_1_animation.gif", writer="imagemagick", fps=20)
plt.show()
Snapshots:
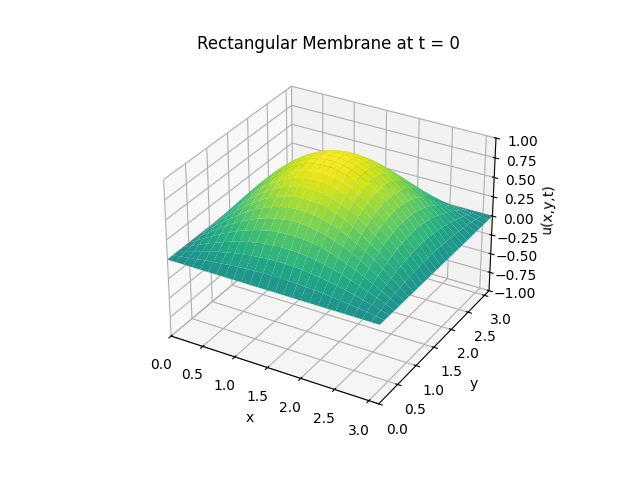
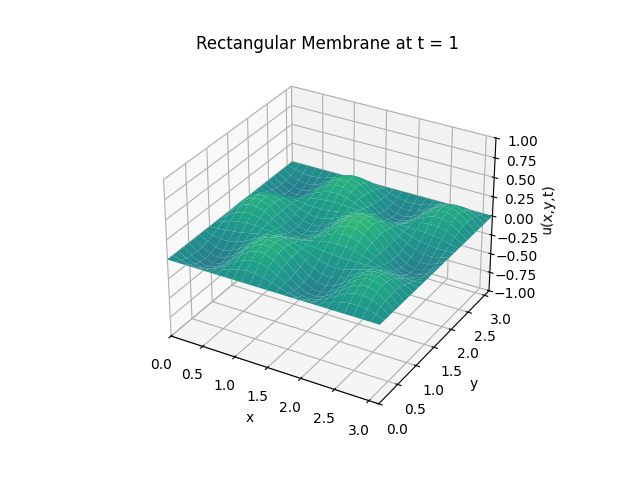
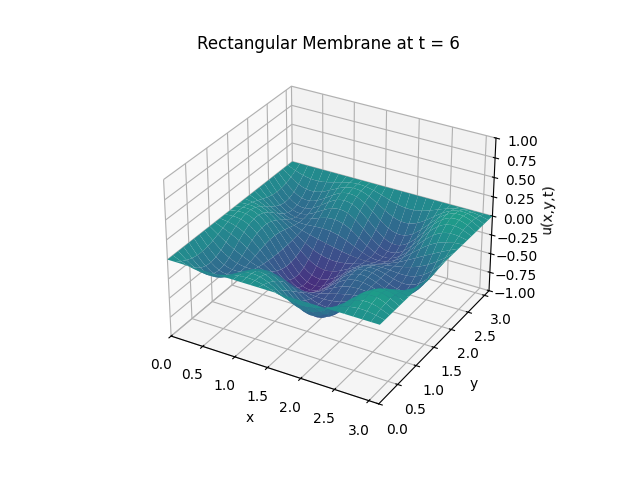
Example 2
...
$$\left\{\begin{align*}
u_{tt} - \pi^2 (u_{xx} + u_{yy}) = 0, 0 < x < 1, 0 < y < 2, t > 0, \\
u|_{t=0} = \cos{\left(\left(x + \frac{1}{2}\right)\pi\right)} \cos{\left(\frac{\pi}{2}\left(y + 1\right)\right)}, u_t |_{t=0} = 0, 0 \leq x \leq 1, 0 \leq y \leq 2, \\
u|_{x = 0} = 0, u|_{x = 1} = 0, 0 \leq y < 2, t \geq 0, \\
u|_{y = 0} = 0, u|_{y = 2} = 0, 0 \leq x \leq 1, t \geq 0.
\end{align*}\right.$$
Solution with Fourier method:
$$u(x, y, t) = \sum_{n, m = 1}^{\infty} \left(A_{n, m} \cos{\sqrt{\lambda_{n, m}} t} + B_{n, m} \sin{\sqrt{\lambda_{n, m}} t} \right) \sin{\pi n} x \sin{\pi m} y,
$$
where
$$\lambda_{n, m} = \pi^2 (n^2 + m^2)
$$
and
$$B_{n, m} = 0.
$$
$$A_{n, m} = 2 \int_{0}^{1} \cos{\left(\left(x + \frac{1}{2}\right)\pi\right)} \sin{\pi nx} \mathrm{d}x \int_0^2 \cos{\left(\frac{\pi}{2}\left(y + 1\right)\right)} \sin{\pi my} \mathrm{d}y.
$$
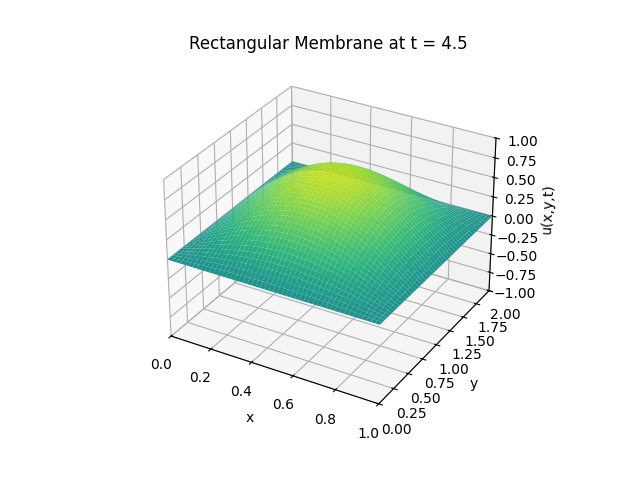
Visualising the solution for \(t \in [0, 6]\) with the partial sum
$$\tilde{u}(x, y, t) = \sum_{n, m = 1}^{30} A_{n, m} \cos{\sqrt{\lambda_{n, m}} t} \sin{\pi n} x \sin{\pi m} y.
$$
Animation:
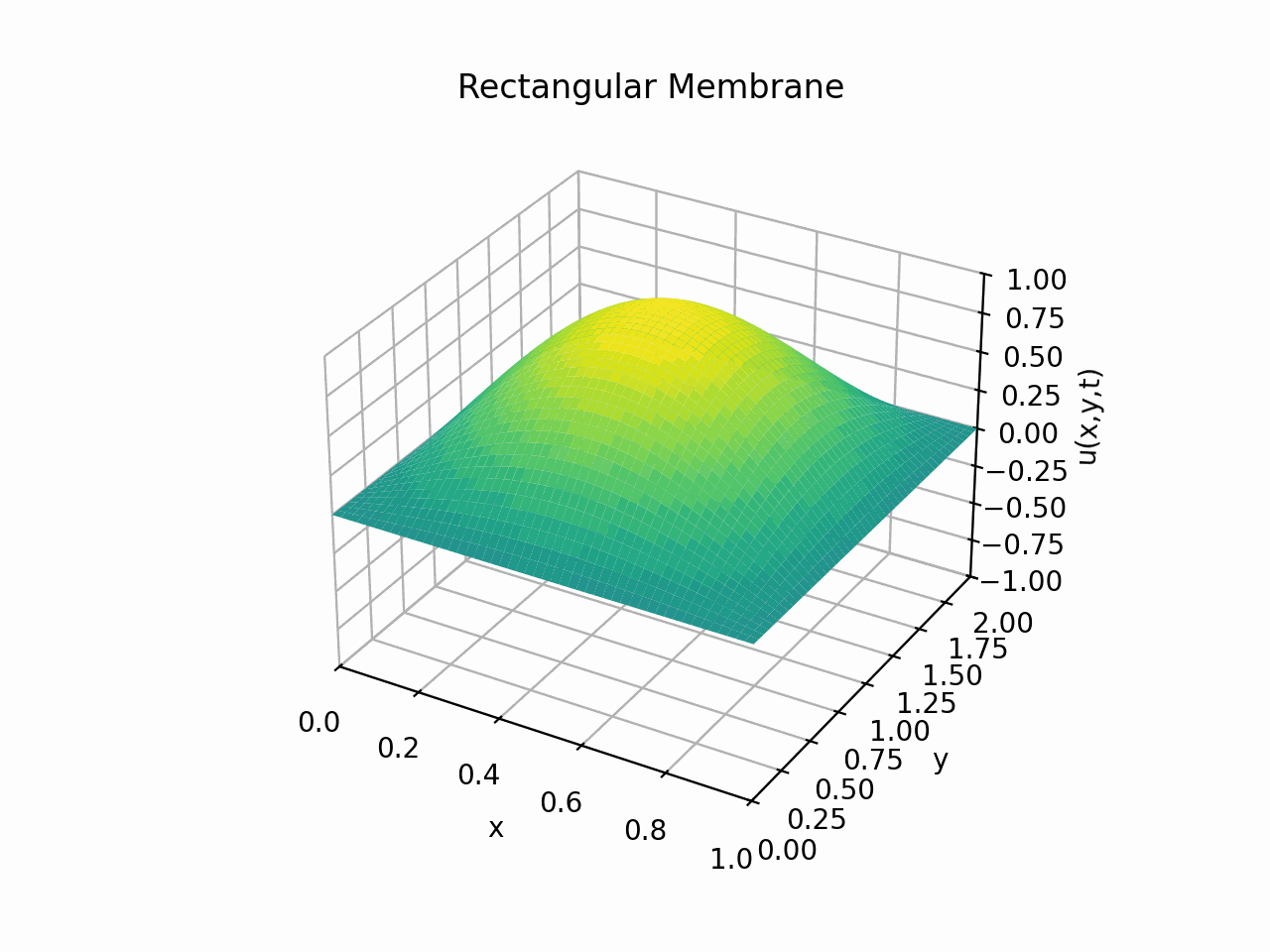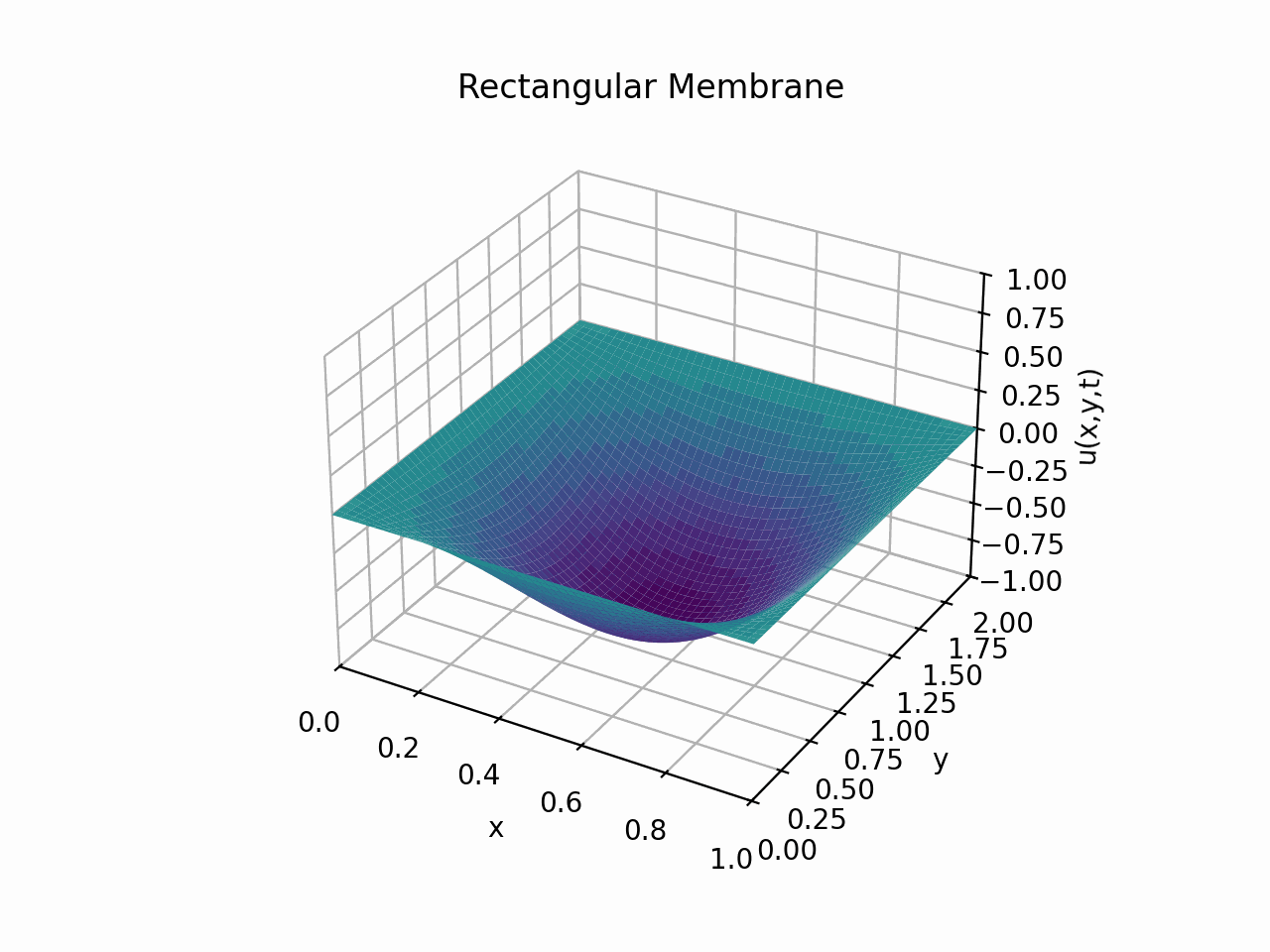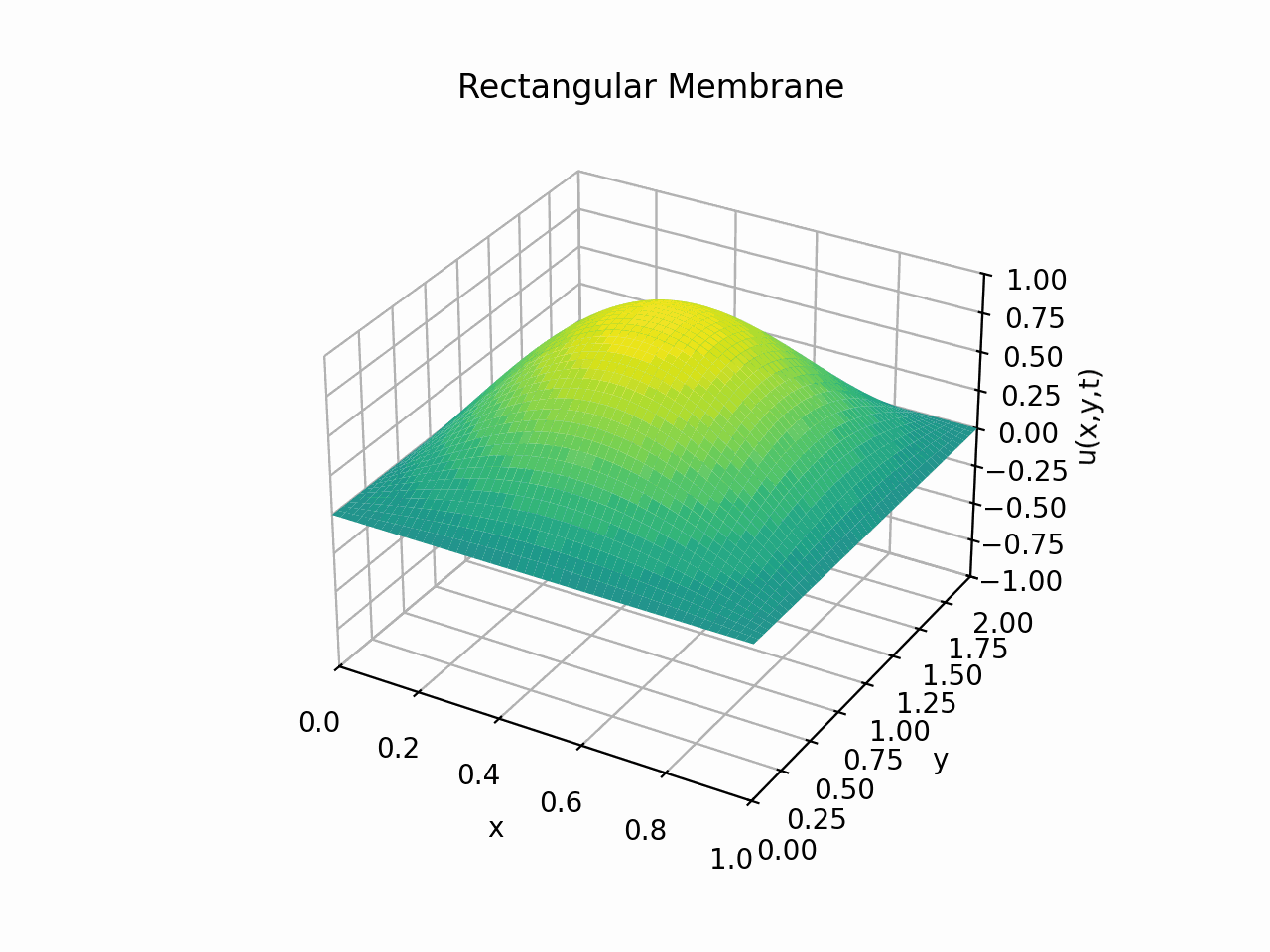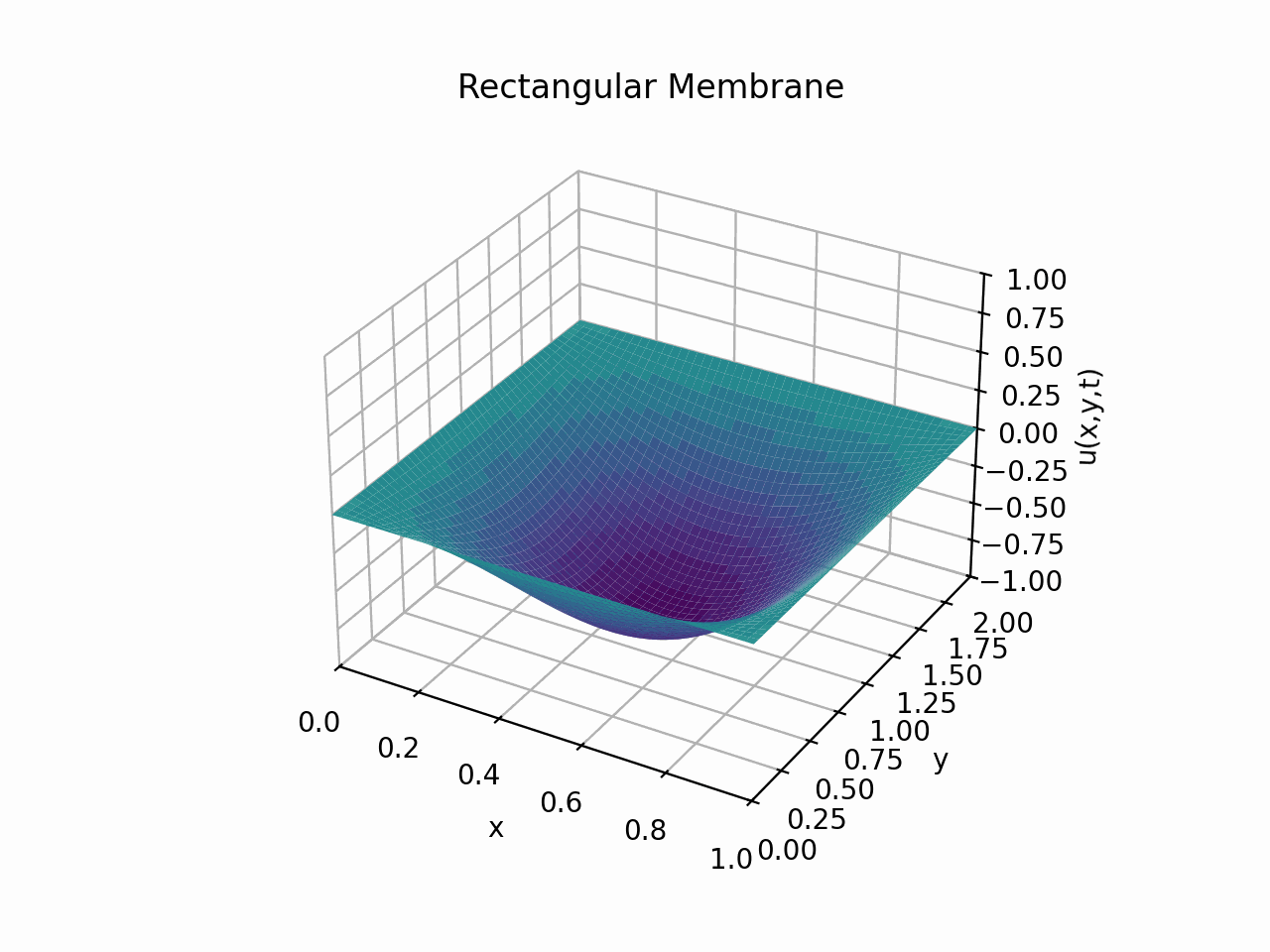
Click to expand code
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
def rectangular_membrane_2(a: float = 1, b: float = 2, c: float = np.pi, tmax: int = 6):
t = np.linspace(0, tmax, 100) # Time points for animation
x = np.linspace(0, a, 50) # x grid
y = np.linspace(0, b, 50) # y grid
X, Y = np.meshgrid(x, y)
# Define the solution function
def solution(x, y, t):
z = 0
for n in range(1, 31):
for m in range(1, 31):
lambda_nm = np.pi**2 * (n**2 / a**2 + m**2 / b**2)
# Compute the coefficient Anm
xx = np.linspace(0, a, 100)
yy = np.linspace(0, b, 100)
Anm = (
4
* np.trapezoid(
np.cos(np.pi / 2 + np.pi * xx / a) * np.sin(n * np.pi * xx / a),
xx,
)
* np.trapezoid(
np.cos(np.pi / 2 + np.pi * yy / b) * np.sin(m * np.pi * yy / b),
yy,
)
/ (a * b)
)
z += (
Anm
* np.cos(c * np.sqrt(lambda_nm) * t)
* np.sin(n * np.pi * x / a)
* np.sin(m * np.pi * y / b)
)
return z
# Set up the figure and axis for animation
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
ax.set_xlim(0, a)
ax.set_ylim(0, b)
ax.set_zlim(-1, 1)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("u(x,y,t)")
ax.set_title("Rectangular Membrane")
# Update function for FuncAnimation
def update(frame):
ax.clear()
Z = solution(X, Y, frame) # Compute the new Z values
ax.plot_surface(X, Y, Z, cmap="viridis", vmin=-1, vmax=1)
ax.set_xlim(0, a)
ax.set_ylim(0, b)
ax.set_zlim(-1, 1)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("u(x,y,t)")
ax.set_title("Rectangular Membrane")
# Create and save the animation
anim = FuncAnimation(fig, update, frames=t, interval=50)
anim.save("rectangular_membrane_2_animation.gif", writer="imagemagick", fps=20)
plt.show()
Snapshots:
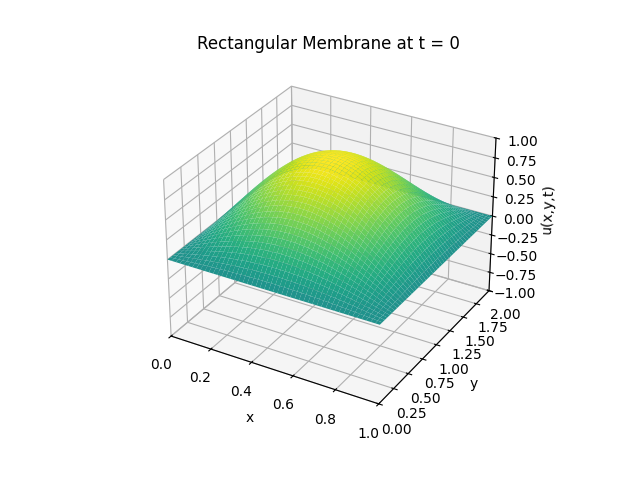
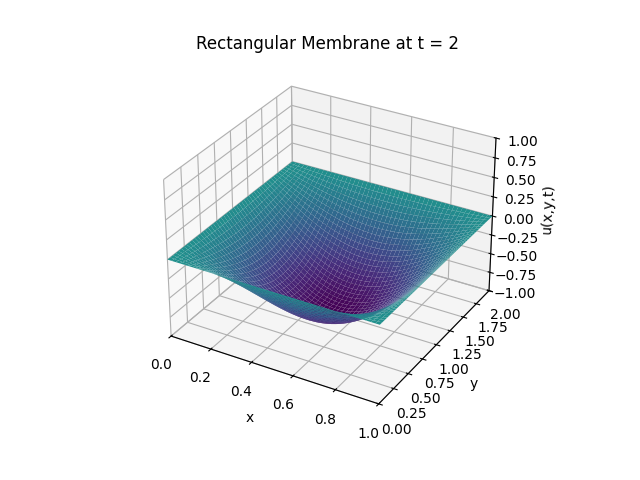
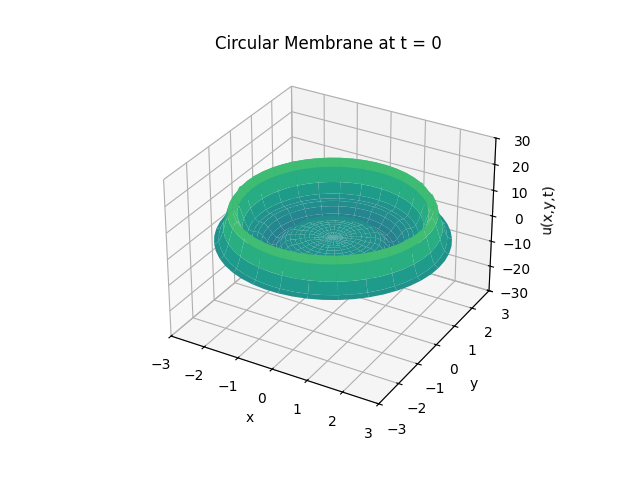
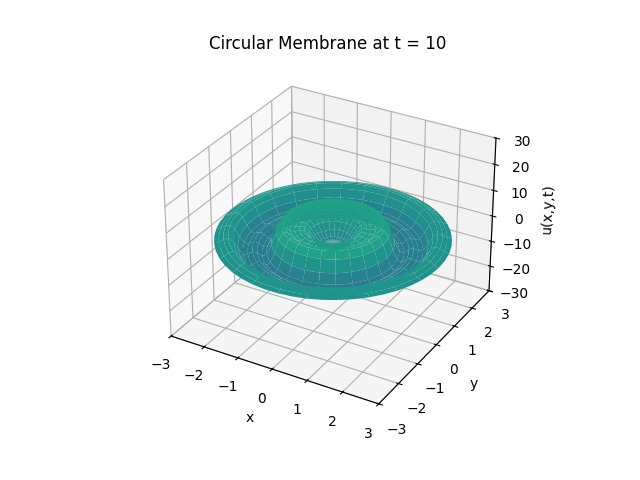
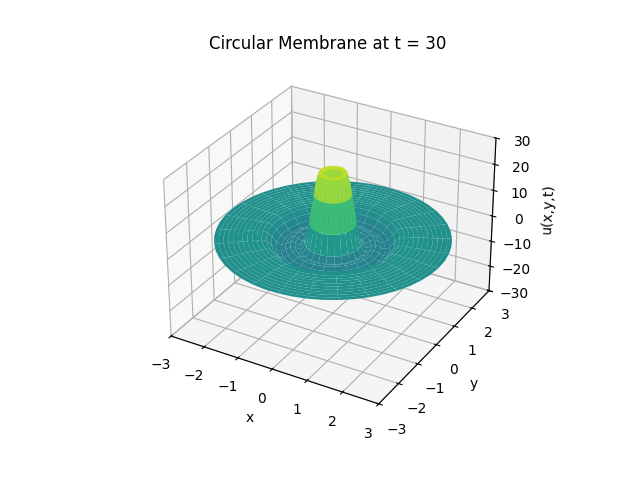
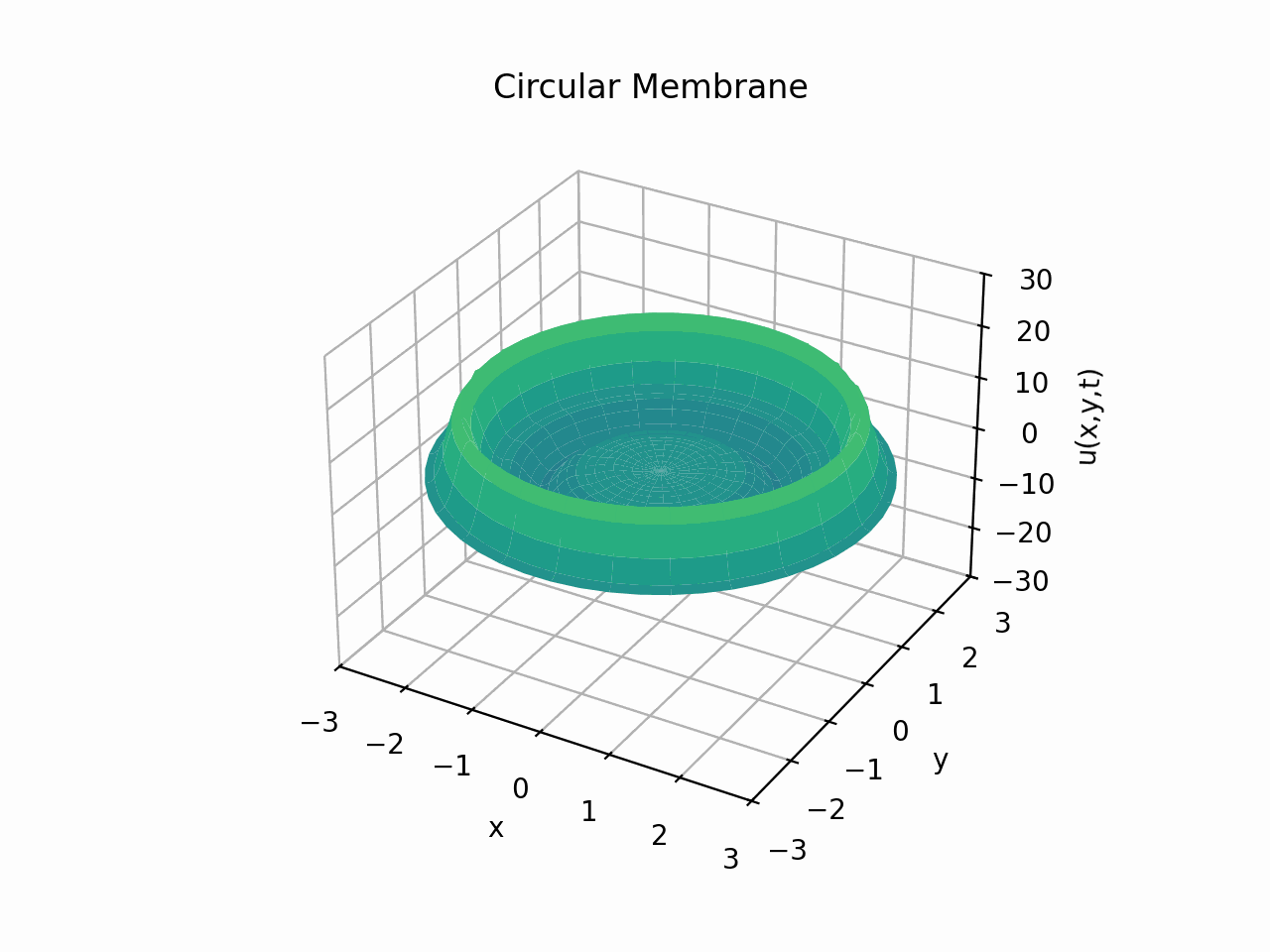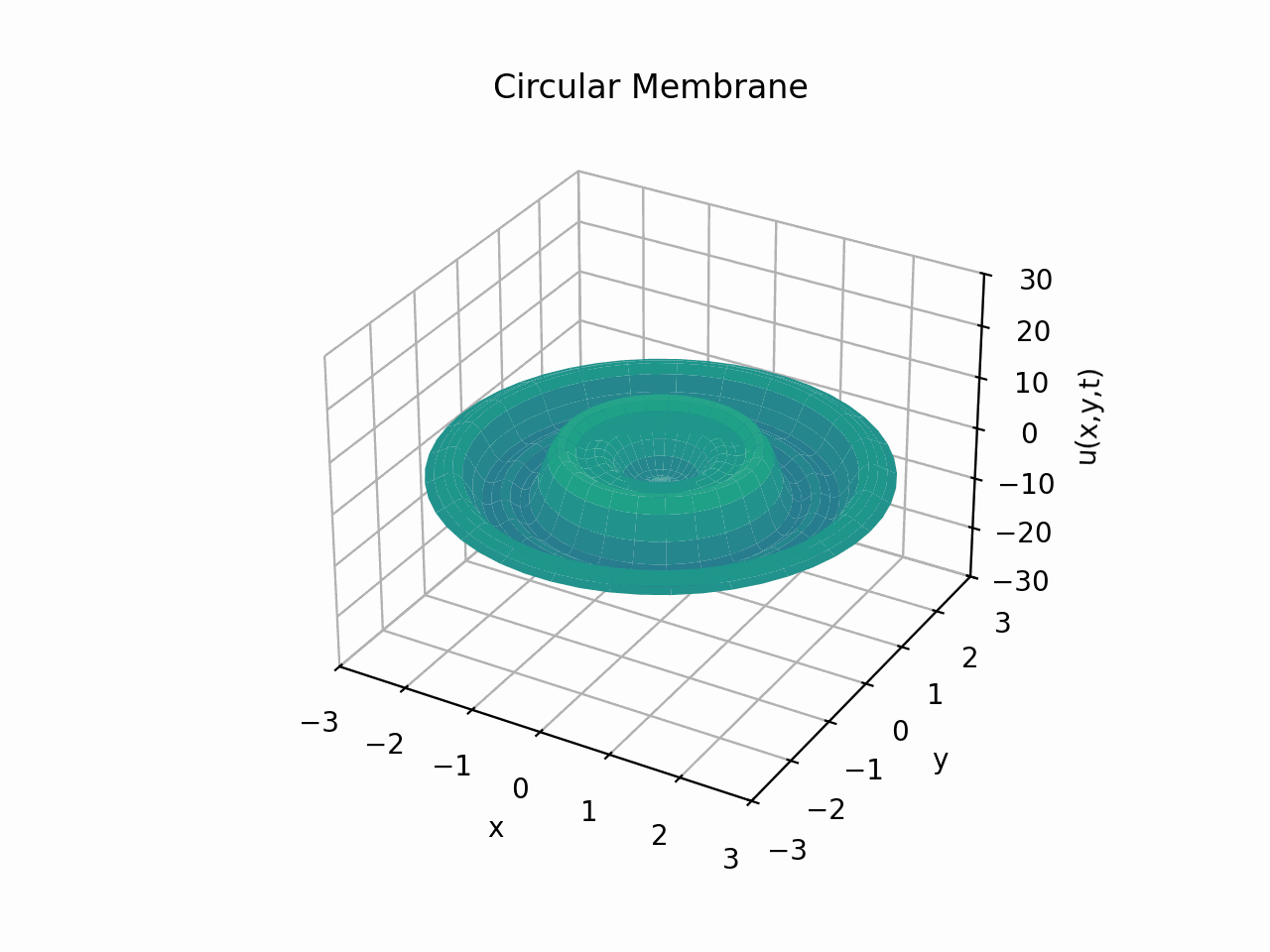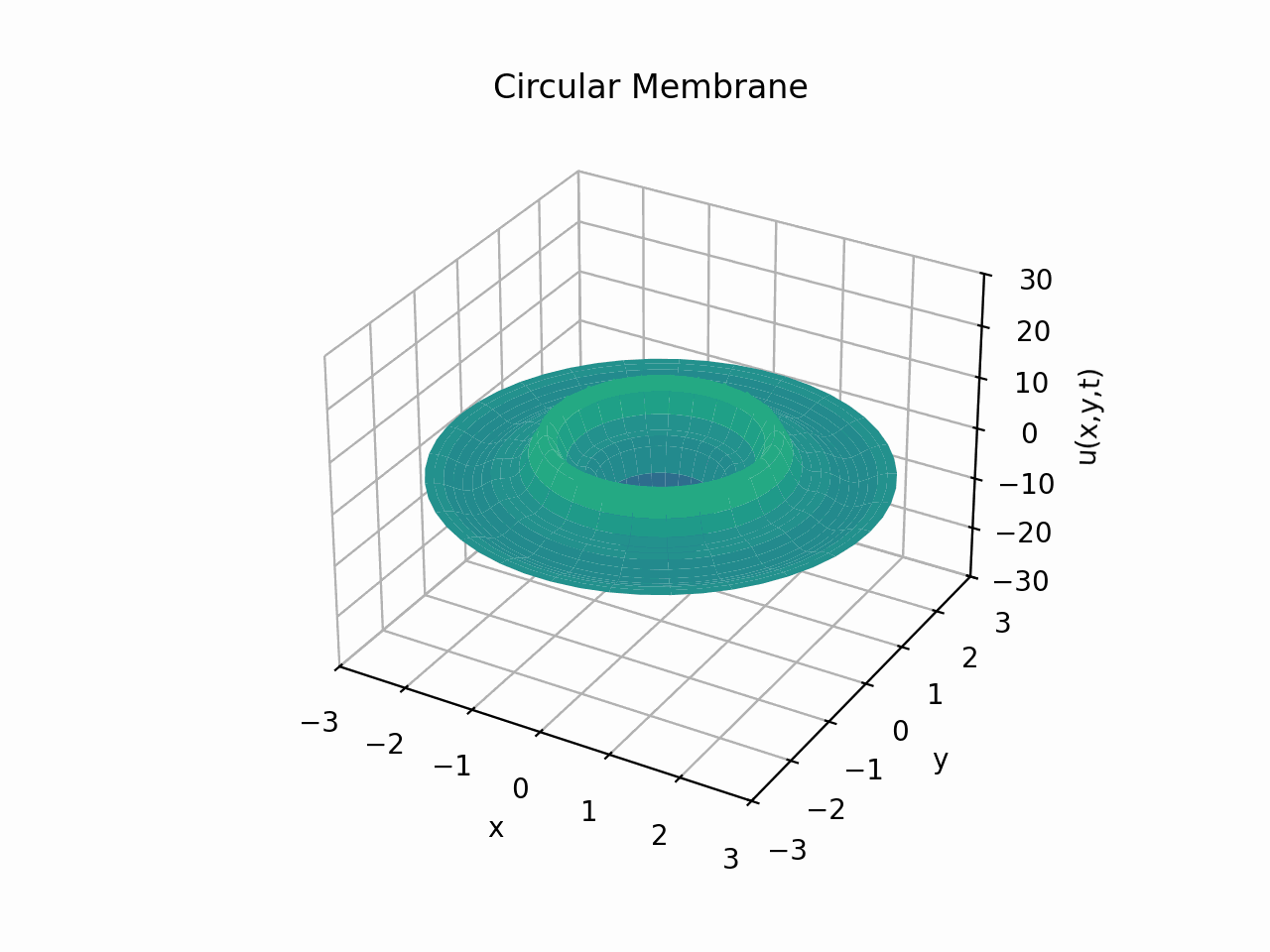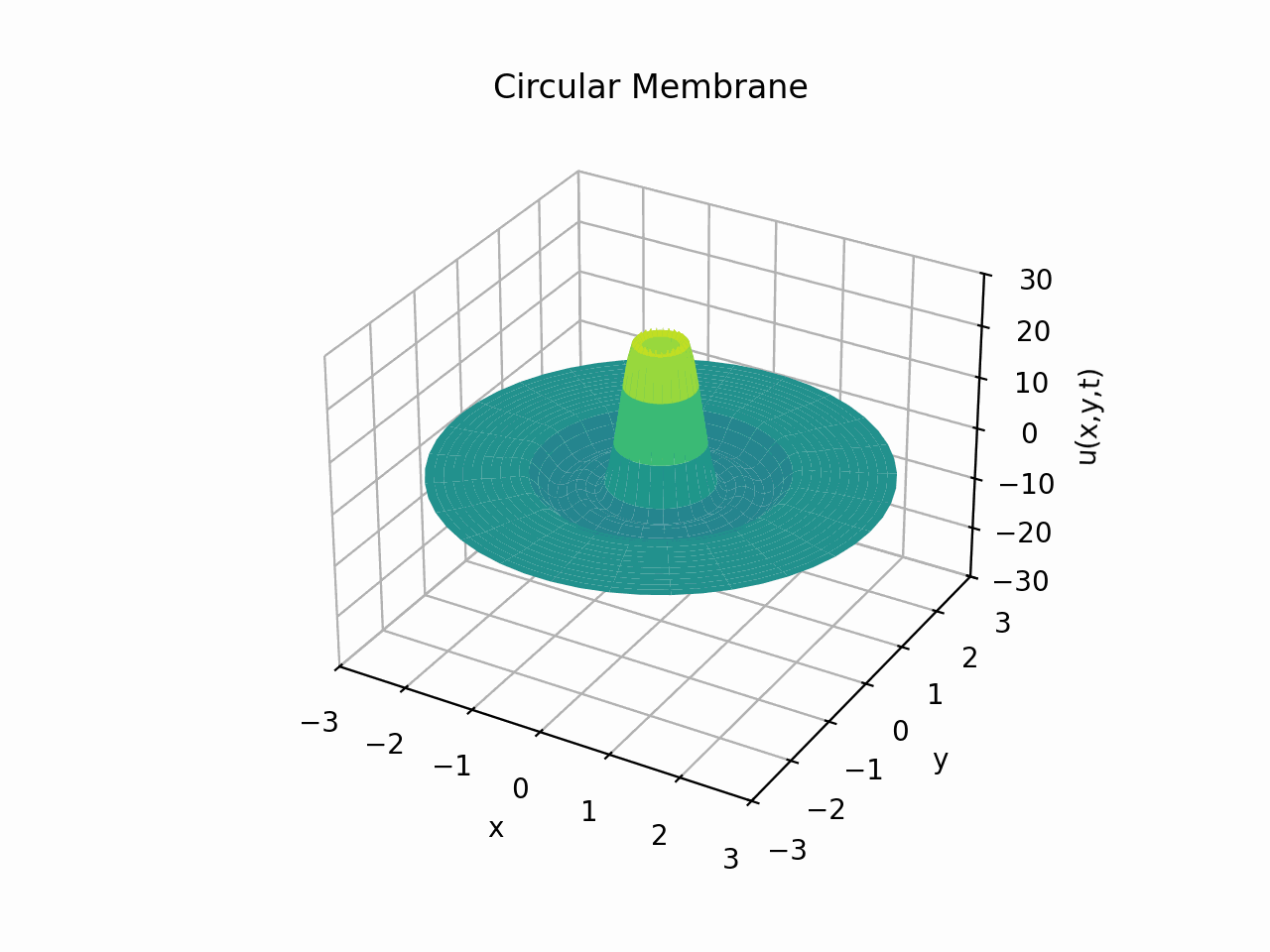
Circular Membrane
Pass
$$\left\{\begin{align*}
u_{tt} - \frac{1}{4} (u_{xx} + u_{yy}) = 0, x^2 + y^2 < 9, t > 0, \\
u|_{t=0} = (x^2 + y^2) \sin^3(\pi \sqrt{x^2 + y^2}), u_t |_{t=0} = 0, x^2 + y^2 \leq 9, \\
u|_{x^2 + y^2 = 9} = 0, t \geq 0.
\end{align*}\right.$$
Fourier method: Change to polar coordinates
$$\left\{\begin{align*}
x = \rho \cos(\varphi), \\
y = \rho \sin(\varphi)
\end{align*}\right.
$$
...
Then the function in the first initial condition \(u |_{t=0}\) becomes
$$\tau(\rho) = \rho^2 \sin^3(\pi \rho)
$$
which is radially symmetric and hence the solution will be also radially symmetric. It is given by
$$u(\rho, t) = \sum_{m=1}^{\infty} A_m \cos{\frac{a \mu_m^{(0)}t}{r}} J_0\left(\frac{\mu_m^{(0)}}{r}\rho\right),
$$
where
$$A_m = \frac{4}{r^2 J_1^2(\mu_m^{(0)})} \int_0^r \rho^3 \sin^3(\pi \rho) J_0\left(\frac{\mu_m^{(0)}}{r}\rho\right) d\rho,
$$
and \(\mu_m^{(0)}\) are the positive solutions to \(J_0(\mu) = 0\).
...
...
Animation:
Click to expand code
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
from scipy.optimize import root_scalar
from scipy.special import jv as besselj
def CircularMembrane(a=0.5, r=3, tmax=30, N=40):
rho = np.linspace(0, r, 51) # Radial grid points
phi = np.linspace(0, 2 * np.pi, 51) # Angular grid points
t = np.linspace(0, tmax, 100) # Time steps
# Find the first 40 positive zeros of the Bessel function J0
mju = []
for n in range(1, N + 1):
zero = root_scalar(
lambda x: besselj(0, x), bracket=[(n - 1) * np.pi, n * np.pi]
)
mju.append(zero.root)
mju = np.array(mju)
# Define the initial position function
def tau(rho):
return rho**2 * np.sin(np.pi * rho) ** 3
# Compute the solution for given R and t
def solution(R, t):
y = np.zeros_like(R)
for m in range(N):
s = tau(R[0, :]) * R[0, :] * besselj(0, mju[m] * R[0, :] / r)
A0m = 4 * np.trapezoid(s, R[0, :]) / ((r**2) * (besselj(1, mju[m]) ** 2))
y += A0m * np.cos(a * mju[m] * t / r) * besselj(0, mju[m] * R / r)
return y
# Create a grid of points
R, p = np.meshgrid(rho, phi)
X = R * np.cos(p)
Y = R * np.sin(p)
# Set up the figure and axis for animation
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
ax.set_xlim(-r, r)
ax.set_ylim(-r, r)
ax.set_zlim(-30, 30)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("u(x,y,t)")
ax.set_title("Circular Membrane")
# Update function for animation
def update(frame):
ax.clear()
Z = solution(R, frame)
ax.plot_surface(X, Y, Z, cmap="viridis", vmin=-30, vmax=30)
ax.set_xlim(-r, r)
ax.set_ylim(-r, r)
ax.set_zlim(-30, 30)
ax.set_title("Circular Membrane")
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("u(x,y,t)")
# Create and save the animation
anim = FuncAnimation(fig, update, frames=t, interval=50)
anim.save("circular_membrane_animation.gif", writer="imagemagick", fps=20)
plt.show()
Snapshots:
